Preliminary results from lifespan studies with E5Harold Katcher has developed a protocol for lab rats using intravenous injection with a blood plasma fraction he calls E5.Three years ago, he announced that treated rats evinced many features of rejuvenation, including improvements in grip strength, endurance, and learning capacity.Two years ago, he announced that treated rats also were epigenetically younger, according to a rodent methylation clock developed by Steve Horvath.This year, with a grant from Heales Foundation, Harold and his partner Akshay Sanghavi have supervised a trial in which older rats were treated with E5 and then allowed to live out their full lifespans so we might know whether epigenetic and phenotypic rejuvenation translate into increased life expectancy.
Just this week, I obtained from them birth and death data for the experimental rats.There were 8 control rats, untreated, all dead, and 8 treated rats, 5 dead and 3 still living.Executive summary of my findings:At any given age, treated rats are 4x less likely to die; but translated into life expectancy, this is less impressive.The rats are living a little longer, but not nearly so much as their methylation age would have predicted.
There is good evidence for compressed morbidity treated rats are healthier later in life, and their deaths are less spread out in time than control rats.Caveats: All rats in the epigenetic experiment were male, while all rats in the lifespan study were female.Also, the protocol was initiated at a later age in the lifespan study compared to the epigenetic study.Raw data:Time is the rats age in days.
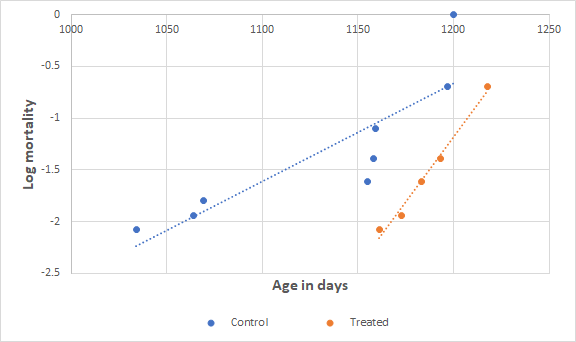
Death =0 indicates that 3 of the rats are still living.Group 1 is control, Group 2 is rats treated with E5.TimeDeathGroup103411106411106911115511115811115911116112117312117902118312119312119711120011120902120902121812How this data is analyzedIt is conventional and, IMO, also reasonable that the data on age at death are interpreted as a probability of mortality.Of course, a greater time period indicates a lower probability of mortality.
Less intuitive, the probability of mortality is based on the number of rats that remain alive at any given time, and not on the total number of rats.Thus, when the first rat dies, its probability of mortality is just , but when the last rat dies, its probability of mortality is 1.0.If a rat is still living it may contribute to the denominator only for rats who died earlier, and not for rats who died later.Using these conventions, I produced the following plot for probability of mortality for the two groups.I have plotted probability of mortality on a log scale because it is an empirical fact that probability of death increases exponentially with age.
This is called the Gompertz rule.If the Gompertz rule holds, then we expect the plot on a log scale to be a straight line.I have drawn the best straight line through the two sets of points.The Gompertz distribution is characterized by two numbers.
One is the base mortality rate, which is related to how early the animals start dying.The other is the mortality rate doubling time.The probability of death doubles again and again over the life of the animals.
A short doubling time indicates that the deaths are all bunched together, and a long doubling time indicates that the deaths are spread out over a broader range of ages.You can see that, compared to controls, the treated rats started dying later and that their mortality doubling time is shorter, with deaths bunched more closely in age.There is substantial uncertainty in these conclusions because of the small number of rats, but there is enough data here to give us confidence in the basic conclusions:Treated rats are less likely to die youngOnce they begin dying, treated rats die faster than controlsIt is unclear from data so far whether maximum lifespan has been increased.We will have a better handle on this question when we see how long the remaining rats live.One more concern about the experiment: Rats are social.Treated rats were housed separately from control rats, 2 or 3 to a cage.
Just like people, rats are more likely to die after their cage mates die.I dont have information about which rats were housed with which, but the death dates show some signs of being bunched together.This social effect could amplify the difference in mortality patterns between treated and control rats.Cox proportional hazardThe most conventional way to analyze contingent survival data is called the Cox proportional hazard model, a relatively new statistical innovation introduced by David R.
Cox in 1972.Many drug treatments and environmental hazards are reported on the basis of Cox models.Result of the Cox model is reported as a hazard ratio, interpreted to mean that if you do X you will be Y% more (or less) likely to die at any given time.The Cox model has the advantage that it is independent of the Gompertz rule or any other assumption about how mortality risk changes over time.It has the disadvantage that it can be misleading if the two different groups have qualitatively different mortality patterns.The Cox model assumes that the difference between the two groups can be expressed as a simple ratio.
If the Gompertz rule holds, a simple ratio translates (using the mortality rate doubling time) into an age change.For example, for humans in modern Western cultures, mortality doubles every 7 years.A Cox ratio of is thus equivalent to rejuvenation by 7 years.Ive done the Cox analysis for Katchers rats because it is conventional, but my opinion is that its assumptions are not satisfied in this case.
The mortality rate doubling time seems to change in the treated rats, indicated by the fact that the slopes of the two lines are different.So interpret the Cox results with this in mind.Cox analysis indicates that the hazard ratio for treated rats is 0.24, meaning that treated rats are 4x less likely to die.The p value = 0.02, indicating confidence in the conclusion that treated rats are living longer than untreated.
Increase in life expectancy is about 7%, which is 85 days for the treated rats.Again, these numbers can change when we see how the remaining 3 rats fare.ConclusionsI have been committed to the idea that methylation clocks provide a real indication of biological age, and that reduction in methylation age will translate to a longer lifespan.MyDataBETA studyis premised on this hypothesis.
There is good theoretical and indirect experimental support for the idea that epigenetics is a driving force behind aging (last weeks blog).On their face, these new results suggest the possibility that methylation age might be decoupled from life expectancy.This is worrisome, but there are other possible interpretations of the situation.We dont have methylation results for the actual animals in the lifespan study.Ive heard there was some mixup sending tissue samples to Horvaths lab for analysis.
There are various reasons these animals may not have responded to E5 treatment as well as the previous group.Katchers rats are our best opportunity to answer this urgent question about a causal link between methylation status and lifespan.Fortunately, he is beginning another lifespan study with both male and female rats, which will follow more closely the protocol of the original study, but will extend in time to offer lifespan data.Unfortunately, the composition of E5 is still proprietary, so the minds of other scientists and the resources of other laboratories are not available to study the remarkable effects reported from E5.
Wider collaboration is urgently needed to study lifespan and also to optimize dosage, timing, and delivery procedures.A collaboration with Johns Hopkins University has been announced by Katchers company (called Yuvan), but we have as yet no details.Possible theoretical interpretationI have written in the past about the Achilles heel of methylation clocks.Aging is like a civil war within the body.
In youth, all metabolic systems are protective, but with age there are systems that attack and destroy the body.Examples are autoimmunity and inflammation.Typically, methylation sites (CpGs) chosen for inclusion in a clock algorithm are correlated with age.There are two possible reasons that an epigenetic change might be correlated with age, depending on which side of the civil war the system is fighting for.
A given CpG might be associated with a self-destruction gene, or it might be a protective response to the body sensing higher levels of damage.The training algorithm, based on correlation with chronological age or even with mortality, is generally unable to distinguish between these two possibilities.I haveproposed on theoretical groundsthat drivers of aging ought to be more common than responses to damage.Methylation clocks are only useful for evaluating anti-aging interventions to the extent that they are based on genes that drive aging.
Its only through experiments like Katchers that we can learn if our methylation clocks have been contaminated with genes that protect from damage.These preliminary results are a signal of caution and a call for more research, but the evidence is indirect and the results are too thin to change theoretical perspectives now.
Publisher: Josh Mitteldorf ( Read More )

